

Ahmad ibn Muhammad ibn `Adb al-Jalîl al-Sijzî est né en Iran où il a vécu. Fils de mathématicien, il a été actif entre 969 et 998 et a écrit exclusivement des ouvrages de géométrie. En tout, il a rédigé près de 50 traités auxquels se joint une correspondance avec ses contemporains.
Quelques ouvrages :
Sur les propriétés de la coupole hyperbolique et de la coupole parabolique
Sur les propriétés des solides elliptique, hyperbolique et parabolique
Sur la descritpion des sections coniques
Toutes les figures sont à partir du cercle
Sur la construction du compas parfait
Comment concevoir les lignes qui se rapprochent et ne se rencontrent pas
Sur la division de l'angle à côtés droits en trois parties égales
Sur la détermination des deux moyennes par la géométrie
La construction de l'heptagone régulier et la trisection de l'angle
La solution par une méthode universelle d'un problème numérique
Dès le neuvième siècle, la naissance de l'algèbre chez les savants arabes crée un nouveau type de questionnement sur les fondements de cette discipline. En effet, dans la majorités des cas, les équations se résolvent par intersections de coniques (ellipse, parabole, hyperbole).
Par exemple :
Pour résoudre l'équation (en notation moderne) : x3 + 2x2 + x = 4
Cela revient à : x (x2 + 2x + 1) = x (x + 1)2 = 4
Qui peut s'écrire aussi : 4/x = (x + 1)2
Donc, les solutions, si elles existent sont les points d'intersection de :
l'hyperbole H(en rouge): H(x) = 4/x
et de
la parabole P(en bleu): P(x) = (x + 1)2
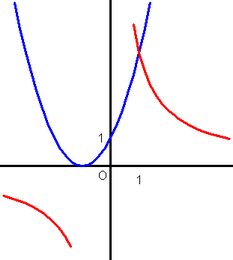
Le tracé point par point des coniques est connu depuis l'Antiquité (voir les Coniques d'Appolonius de Perge en particulier), et cette construction est suffisante pour l'étude des propriétés de ces courbes. Mais au neuvième siècle, la nécessité de concevoir les intersections change radicalement la donne car l'existence des solutions repose sur la continuité des différentes courbes en jeu. Il n'est évidemment pas question à cette époque de définir la continuité à partir de la construction des réels comme c'est le cas depuis le dix-neuvième siècle avec les travaux de Cantor et Dedekind. La méthode choisie consiste à associer une courbe à un instrument permettant de la tracer effectivement. À l'image de la règle et du compas qui permettent de tracer des droites et des cercles et d'en justifier la continuité, il restait à inventer un instrument permettant de tracer des coniques, et si possible, toutes. L'intérêt n'est pas seulement mathématique car les coniques servent aussi dans des domaines techniques comme la construction des astrolabes et des cadrans solaires.

Dans son ouvrage Sur la description des sections coniques, al-Sijzi reprend l'ensemble des procédés mis en place par ses prédécesseurs. Ainsi, après l'évocation des travaux d'auteurs comme les frères Banu Musa, ou d'Ibn Sinan, dans son Traité sur la construction du compas parfait qui est le compas du cône, il s'intéresse à un nouvel instrument, inventé peu de temps auparavant par al-Quhi : le compas parfait.
Comme il n'annonce lui-même dans les premières pages de son traité, il veut «construire un compas à l'aide duquel on obtient les trois sections du cône.» Remarquant que toutes les sections coniques peuvent être obtenues à partir d'un cône droit (selon la position du plan de coupe), il propose trois constructions possibles pour le compas parfait. Voici la première, les deux autres reposant sur les mêmes principes.
«Il nous faut maintenant montrer comment façonner un compas à
l'aide duquel on puisse tracer ces sections. Façonnons une tige ; soit
AB. Plaçons à son sommet un tube ; soit AN. Lions à l'extrémité de
celui-ci un autre tube ; soit AS. Il nous est possible de réaliser cela
à l'aide d'une cheville, ou de tout autre chose, de sorte que le tube
AN tourne autour de la tige AB et que le tube AS tourne avec lui ; et
cela pour faire une tige qui glisse à l'intérieur du tube AS et sur
laquelle se trouve

«Nous construisons ensuite un arc tel que GE sur la tige AB, dont un point est sur un appui par lequel les côtés G et E s'élèvent et s'abaissent vers le sommet et la base ; on le construit facilement, soit par un ressort, soit en faisant glisser une règle dans une encoche ou par tout autre procédé facile qui nous convienne.» [1] p.286-288
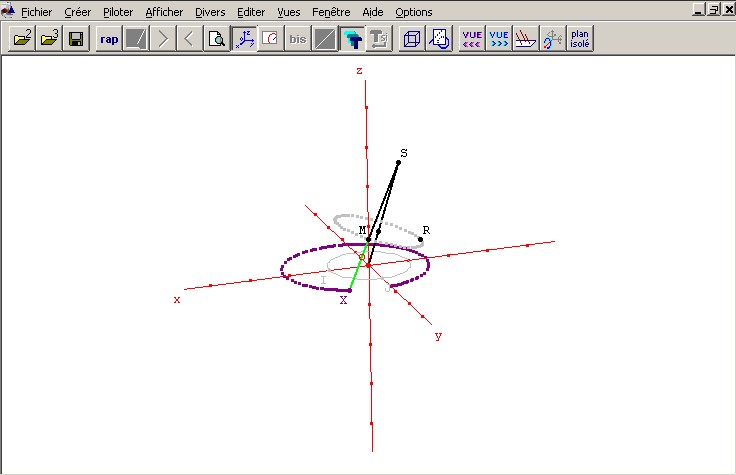
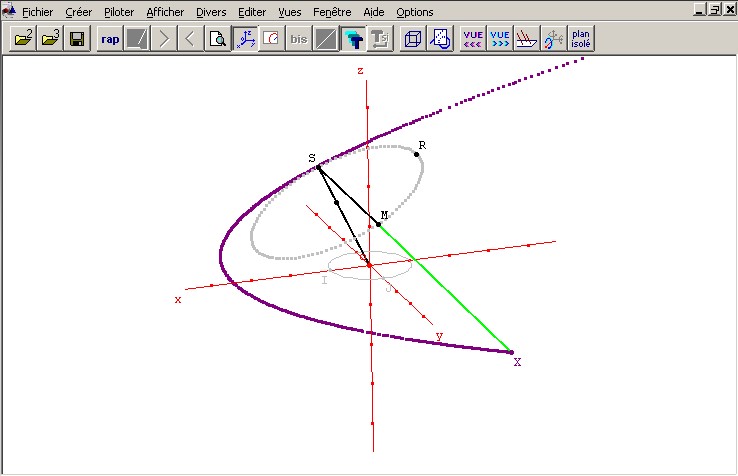
Activité : Télécharger la figure Geospace (figure) et la manipuler afin de déterminer les différents types de courbes que l'on peut obtenir avec cet instrument.
Les points S, R, et M sont mobiles (les deux premiers définisant les paramètres d'ouverture du compas).
Pour tracer, dans le menu Afficher, selectionner Mode Trace (Bascule). Déplacer ensuite le point M. Rebasculer le mode Trace pour effacer la figure.
Pour voir la feuille de dessus, dans le menu Vues, selectionner Vue standard avec oxy de face (F8). Utiliser le même menu pour retrouver la vue initiale (ou avec CTRL+F1).
Dans ses traités, al-Sijzi part, comme ses prédécesseurs, du cône droit et des différents positions du plan de coupe. Il obtient la classification suivante (déjà présente sous une forme un peu différente chez al-Quhi).
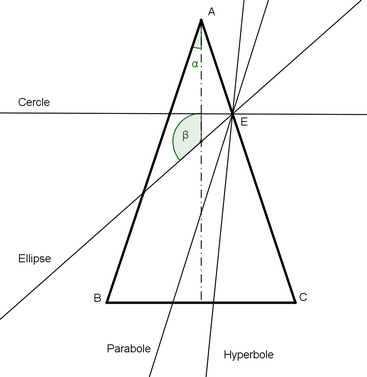
Si β = 90°, la section est un cercle
Si α + β < 180°, la section est une ellipse
Si α + β = 180°, la section est une parabole
Si α + β > 180°, la section est une hyperbole
La nature des différentes sections n'est donc pas difficile à déterminer, par contre les calculs deviennent vite très compliqués si l'on souhaite trouver les angles correspondant à une conique en particulier.
Les calculs étaient évidemment à la portée d'un savant comme al-Sijzi, cependant, l'objectif de l'étude du compas parfait n'est pas simplement de pouvoir tracer des coniques. Comme tout instrument mathématique, ce compas est aussi un outil théorique et un instrument de découverte de notions nouvelles. Le lien entre le cercle et l'ellipse est assez évident. La construction de l'ellipse par affinité orthogonale et la formule de l'aire est connue depuis longtemps. Par contre, quels liens existent entre le cercle et la parabole ou l'hyperbole ? À ce moment de l'étude, l'outil pratique devient un instrument de découverte et comme le souligne al-Sijzi lui-même :
«J'avais toujours réfléchi à l'existence d'un rapport entre ces deux figures et le cercle et à leur similitude et cherché à le saisir ; or la connaissance de ceci ne m'en a été possible qu'une fois appris comment faire tourner le compas conique suivant les positions des plans.» [1] p.254
paragraphe en cours de réécriture...
[1] Œuvre mathématique d'al-Sijzî, R.Rashed, Les Cahiers du Mideo, 3, Louvain-Paris, Éditions Peeters, 2004.
[2] Histoire des sciences arabes, 3 vol., Paris : Le Seuil, 1997.
[3] Le développement de la géométrie aux IXe-XIe siècles, Abu Sahl al-Quhi, P.Abgrall, Albert Blanchard, 2004.
[4] Geometry and dioptrics in classical islam, R.Rashed, al-Furqan, 2005.
[5] Le
tracé continu des sections coniques à la Renaissance : applications
optico-perspectives, héritage de la tradition mathématique arabe, D.Raynaud, Arabic Sciences and Philosophy, 17 (2007), pp.299-345.
